"bob and john" (bobandjohn)
04/13/2015 at 11:47 • Filed to: None
1
17|
"bob and john" (bobandjohn)
04/13/2015 at 11:47 • Filed to: None | 1
| 17 |
I am trying to figure out how to go from normal-tangential acceleration and re-write it as radial-transverse. and I can not for the life of me figure it out.
Help?
Coty
> bob and john
04/13/2015 at 11:57 |
|
I understand all those words individually.
desertdog5051
> bob and john
04/13/2015 at 11:58 |
|
http://physics.tutorvista.com/motion/tangent…
With-a-G is back to not having anything written after his username
> bob and john
04/13/2015 at 11:58 |
|
I need to know more of the specific geometry...
RamblinRover Luxury-Yacht
> bob and john
04/13/2015 at 12:00 |
|
Given that I have not encountered those terms exactly as you use them, are you trying to convert a tangential acceleration applied at the extremity of a circle to axial acceleration in rad/s^2 or something like that?
|
bob and john
> desertdog5051
04/13/2015 at 12:02 |
|
tried that, its only explaining them, not showing me how to change them.
|
desertdog5051
> bob and john
04/13/2015 at 12:03 |
|
I got nothing.
|
bob and john
> With-a-G is back to not having anything written after his username
04/13/2015 at 12:05 |
|
Short-throw Granny Shifter is 2 #blessed 2b stressed
> bob and john
04/13/2015 at 12:05 |
|
I think the approach is to use trig functions to break the vector into components. Are you trying to express an acceleration function in parametric or polar coordinates?
|
bob and john
> With-a-G is back to not having anything written after his username
04/13/2015 at 12:06 |
|
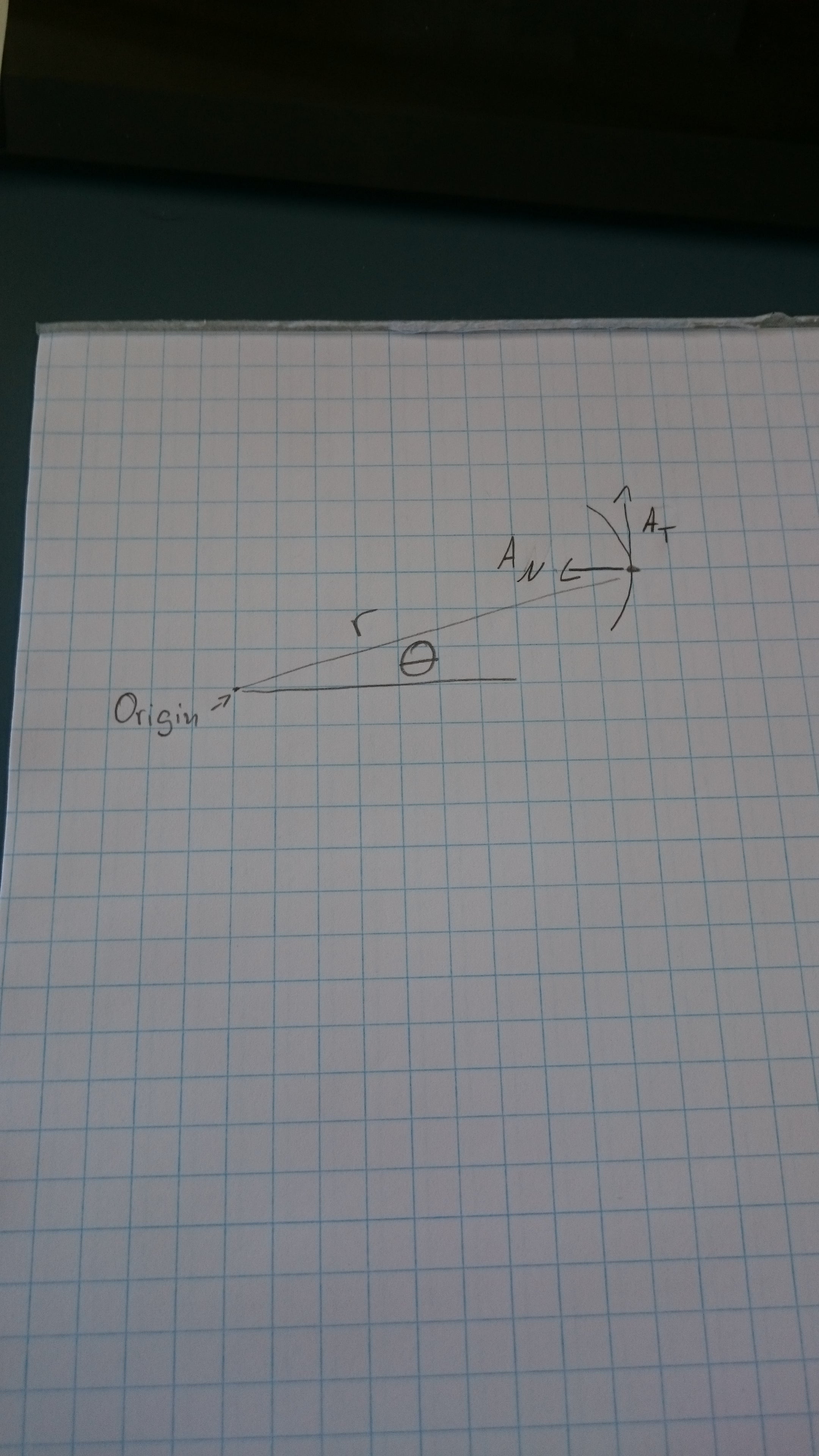
so say i have particle P mvoing along a path and I have A-tangential and A normal. I want to know how to change it into A radial and A (theta)
|
bob and john
> RamblinRover Luxury-Yacht
04/13/2015 at 12:08 |
|
no, I have tangential and normal acceleratation. I need to express them as a radial and transverse acceleration from a origin
|
RamblinRover Luxury-Yacht
> Short-throw Granny Shifter is 2 #blessed 2b stressed
04/13/2015 at 12:11 |
|
He doesn't have to use trig functions if the accelerations really are normal and tangential. It's drawn wrong in that respect.
|
RamblinRover Luxury-Yacht
> bob and john
04/13/2015 at 12:17 |
|
The normal acceleration is the radial acceleration. The transverse acceleration is the tangential acceleration /pi*r, if I've got that right. In other words, something accelerating tangentially at roughly 3.14 (bear with me, number chosen for convenience) and with r=1, it's accelerating at 1 radian per second per second. If I've got that right. This is just a coordinate system conversion, if I'm not mistaken - if you were actually trying to solve for some of these in terms of one another or didn't have the acceleration on the outside broken down already, it would be different.
|
bob and john
> RamblinRover Luxury-Yacht
04/13/2015 at 12:21 |
|
I get what your talking about, but its not what I need. Look at one of my other replies and you;'ll see a diagram
450X_FTW
> bob and john
04/13/2015 at 12:24 |
|
(reads title) OOO this will be good, I personally enjoy physics.
(reads question) fuck it was 10 years ago I was reading problems like that. No help.
|
RamblinRover Luxury-Yacht
> bob and john
04/13/2015 at 12:35 |
|
I saw the diagram before I made my response. I still don't understand what you need if not that. What you have drawn has the tangential acceleration and normal acceleration taking place along the cartesian x/y somewhere other than the x-axis, which I assumed was wrong, because they would otherwise not actually be tangential and normal. Do you mean to say that there's an acceleration with those tangential and normal components which isn't actually acceleration taking place with respect to that origin and radius, but remains with those x and y components through translation - so would need to vary depending on angle? I don't think that's possible to be what you're being asked. If it is, your teacher shouldn't describe such a force as *being* tangential/normal except with caveats... and would presumably be trying to fuck you over, because that would be a dick question.
Phyrxes once again has a wagon!
> bob and john
04/13/2015 at 12:39 |
|
AP Physics teacher checking in, I know I don't use those terms for my students but I am only doing basic rotational motion with them. For your particular question are you looking for a calculus based or algebra based solution. I'll look through my material (I have an off period right now) and get back to you.
nctrns
> RamblinRover Luxury-Yacht
04/13/2015 at 12:52 |
|
Or he phrases the question wrong.
If we can assume that the sketch he did contains all data, then the only thing he can do is to use trig to convert the acceleration into tangential acceleration (as in perpendicular to the radius, then angular acceleration = At/r