 "Torquelife" (torquelife)
"Torquelife" (torquelife)
04/15/2015 at 16:30 • Filed to: None
 6
6
 12
12
 "Torquelife" (torquelife)
"Torquelife" (torquelife)
04/15/2015 at 16:30 • Filed to: None |  6 6
|  12 12 |
Furious Seven: exotic cars, exotic locales, extended vehicular warfare, cars being parachuted out of a plane...and an obscure, modern-day hypercar literally flying through buildings? That's different. That's legit. Wait, is that actually possible?
!!! UNKNOWN CONTENT TYPE !!!
Find more !!!error: Indecipherable SUB-paragraph formatting!!! content at !!!error: Indecipherable SUB-paragraph formatting!!! and on Twitter !!!error: Indecipherable SUB-paragraph formatting!!! .
!!! UNKNOWN CONTENT TYPE !!!

!!! UNKNOWN CONTENT TYPE !!!
Last weekend, I was one of the legions of theatergoers worldwide who contributed to Furious Seven 's record-shattering $384 million opening weekend worldwide box office haul ($143.6 million in US box office collections, $240 million internationally - source).
The seventh Fast and Furious installment followed the same theme as the last few movies - exotic cars, exotic locales, just the flimsiest outline of a plot (sometimes, not even that), and some gloriously outlandish stunts. There's extended vehicular warfare on offer here, plus some cars being parachuted out of a plane, and a Lykan HyperSport literally flying through skyscrapers.
The latter scene was the one that really caught my eye when the Furious Seven trailer premiered. The series has mostly handled large action sequences pretty well, especially since Tokyo Drift , so it wasn't a surprise to see extended automotive combat scenes set in the streets of LA and on Pikes Peak mountain in Colorado. And a rally-prepped '68 Charger parachuting out of a plane is right up the alley of a movie franchise that once turned an old Yenko Camaro into a big-block projectile to destroy a fleeing yacht. But an obscure, modern-day hypercar literally flying through buildings? That's different. That's legit. That's...wait, is that actually possible?
Let's cue some background info (mild spoiler alert): The crew needs to break into a billionaire's penthouse in the Etihad Towers, the tallest residential building in Dubai, to steal a flash drive. Conveniently, this flash drive is stashed inside a $3.4 million Lykan HyperSport, one of seven in the world, that is parked in a vault in his penthouse suite. Naturally, this entire plotline is an excuse for the supercar to take a flying lesson, soaring from one tower to another. Apparently, no amount of exclusivity or diamond-encrusted headlamps can save the brakes on landing, so the car keeps going through the second skyscraper and glides into a third tower. A bit of crashing later, the Lykan falls about 500 feet to an offscreen mechanical death.
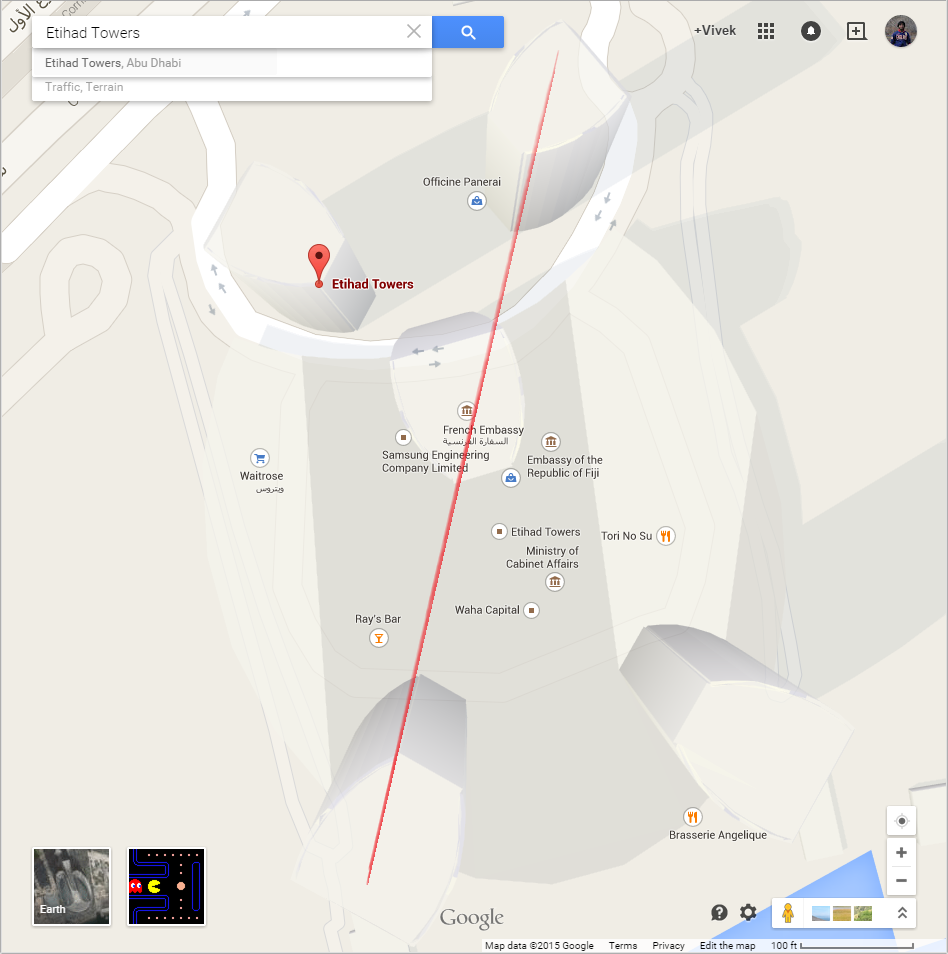
Etihad Towers is a complex of five towers, ranging from 700 to 1000 feet. If we look at the Google Map layout of the five towers, we can see that there are four placed rectangularly and a fifth near the center of them. The two taller towers are in the back, and it's possible to draw a straight diagonal line between the towers at the back left and front right through the middle tower. That's actually a pretty good start, we can assume that this is the route the car took.
The distance between the towers isn't publicly stated from what I can tell, but we can estimate it based on the scale of the layout map above. It's a bit under 200 feet (60 meters) between the first and second towers, and about 100 feet (30m) between the second and third.
The equations behind projectile motion are actually quite simple. Let's assume the car's direction of travel is along the straight line we drew earlier, allowing us to evaluate motion along a simple 2-dimensional coordinate plane. Since our initial velocity is purely in the x-direction, we can simplify the equations:

First, we need to make an assumption around that initial velocity. Based on our handy Google Maps top down view, we can see that there's about 150 feet (45m) of space inside the tower. Let's say that our valiant protagonists had about 80% of that in which to accelerate from an initial velocity of zero, so 120 feet (36m). Lykan claims the HyperSport can do the 0-60 run in a brisk 2.8 seconds, so using that as the rough acceleration curve, we can find the maximum speed the HyperSport can achieve in the allotted 120 feet.
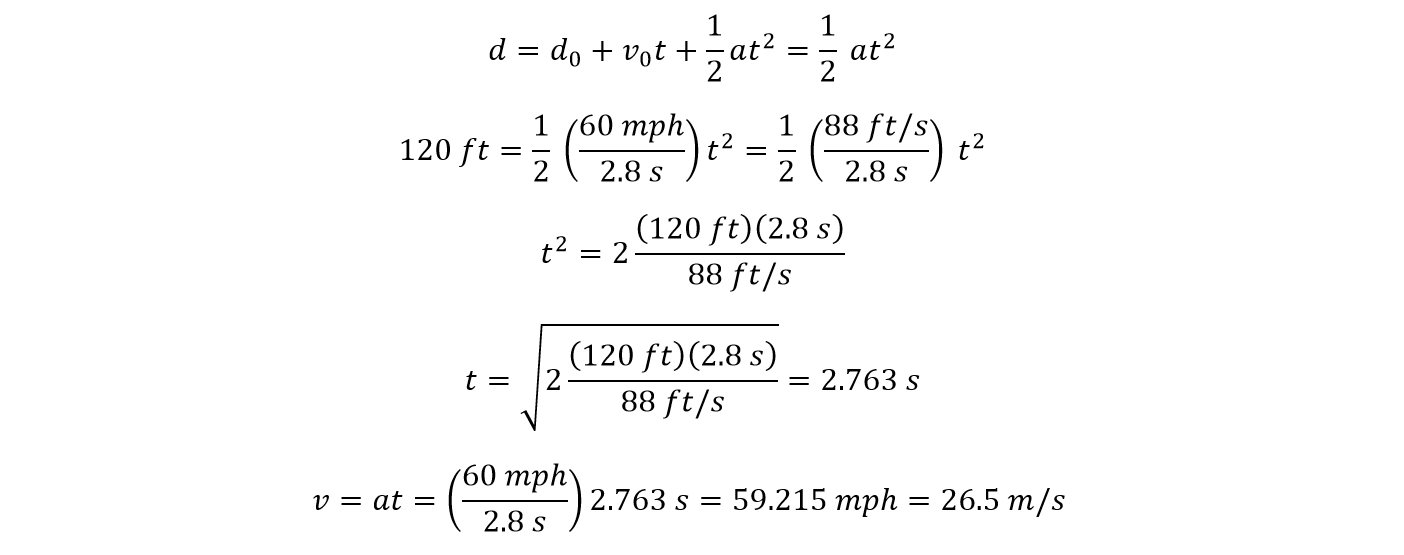
This is easy enough to derive, based on the basic motion equations. As you can see from the calculations, it's at 59.2 miles per hour after 120 feet, which converts to 26.5 m/s. Because we've generally used to basic units of distance and speeds in imperial terms, I've been using them, but from here on, I will be performing all of the calculations in metric units only.
Using the initial velocity as 26.5 m/s, we can look at the 60 meter distance between Tower 2 and Tower 3 and find the time it takes to travel between the two using the same basic distance formula in the x-direction. We can disregard any acceleration (since the car cannot accelerate forward while it is in mid-air), which leaves us with:

2.264 seconds. Not too shabby. In movie time, it takes a lot longer, due to the slow-motion and multiple angle cutaway used by the director, but at least you know that if you try it for real, your flight time will be brief (but memorable!)
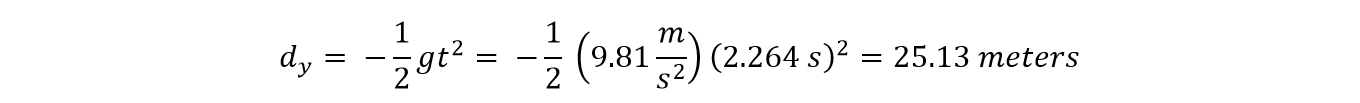
During this time, the car will drop 25.13 meters, so somewhere between four and five stories - it's safe to assume here that the upper stories of these towers all have higher than normal ceilings.
If we say that Tower 3 also measures 45 meters from one side to the other, and that only half of that is used for acceleration due to the landing, the initial attempt to brake, and the subsequent ditching of that plan because of the brake failure, we can find what the exit velocity is. A couple of assumptions have to be made - the first being that the Lykan's acceleration curve to 60 mph holds beyond that. This isn't exactly true, but let's just simplify our life and say yes - for a !!!error: Indecipherable SUB-paragraph formatting!!! , the dropoff in the acceleration curve seems to start between 70 and 80 mph and only gets really significant above 100 mph. The second assumption is that the car is still travelling at 26.5 m/s (59 mph) when it starts accelerating again.
Again turning to our distance formula to calculate the amount of time it takes to travel through that 22.5 meters, we can set up a quadratic equation to solve for t.
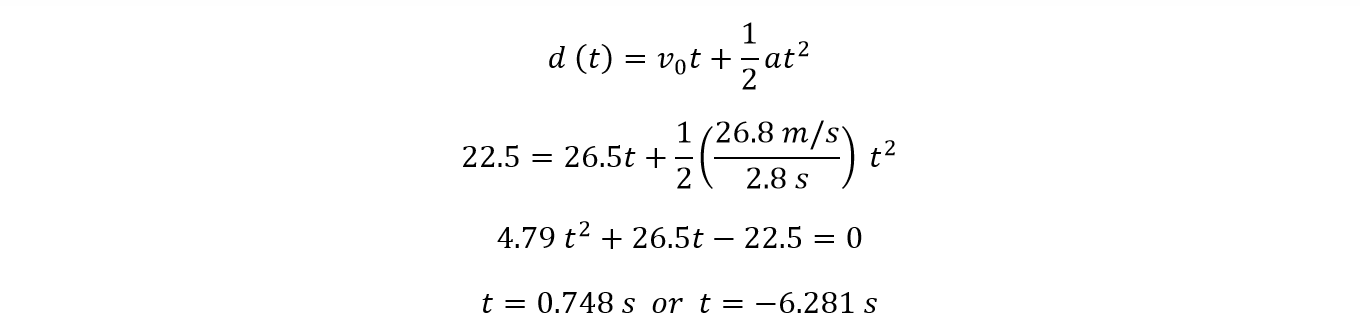
We can ignore the negative value (Dominic Torretto is good, but he's not that good), leaving us with t = 0.748 seconds. Not long, and again not representative of how long this journey takes in the movie.
Plugging that value back into the equation for velocity gives us an exit velocity of 33.67 m/s (75.3 mph). Based on the result of the first tower, we can see that the car should clear this second jump fairly easily. How easily?
For the 30 meter trip between Tower 3 and Tower 4, it should take the Lykan a hair less than 0.9 seconds to cover the distance, falling 3.89 meters in that time. Sounds about right. So, should you ever find yourself in this scenario, you can take heart in knowing that you can very likely jump your hypercar between the Etihad Towers.
It's worth noting here that this calculation does not factor in air resistance. We talked about the drag equation in a previous article, and it serves as the basis for this analysis, but the equations for projectile motion with air resistance are a bit more complex. The drag force is proportional to the square of the velocity, so as the velocity changes, the force (and thus negative acceleration) changes with it quadratically. The basic equation we start with for horizontal motion is this:
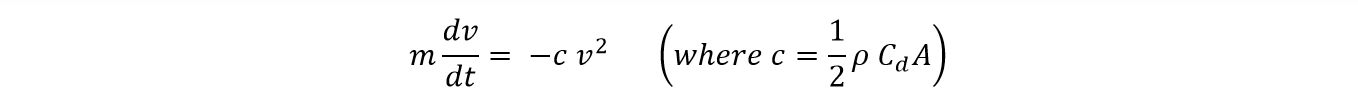
The derivation is a bit lengthy, but after a bit of integration, the equation boils down to this:

For vertical motion, we get a very different looking equation that is based upon the terminal velocity of the car.
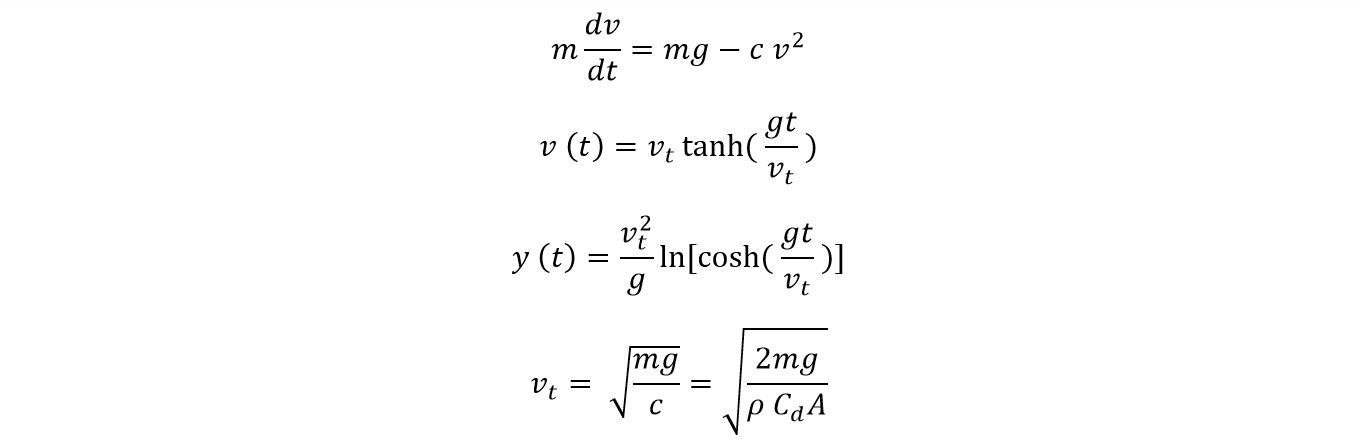
To find the terminal velocity (v_t), we actually turn back to the aerodynamic resistance equation, except rearranged to solve for velocity. In this case, we're looking at the terminal velocity for the bottom of the car; the direction of flow is upwards (opposite of the direction of motion, which is based on gravity), meaning we actually want the drag coefficient and area of the bottom of the car.

Top-down view of the Lykan Hypersport. Image: W Motors ( !!!error: Indecipherable SUB-paragraph formatting!!! ).
Lykan doesn't quote the drag coefficient of the HyperSport, and literally nobody quotes the drag coefficient of the underside of a car. This is because, I suppose, driving them off skyscrapers isn't a typical usecase to design around. As such, we will have to make some assumptions around this. Let's take the drag coefficient and frontal area from a similarly sized and shaped car, like the Gallardo (Cd = 0.35, A = 1.93 sq. meters).
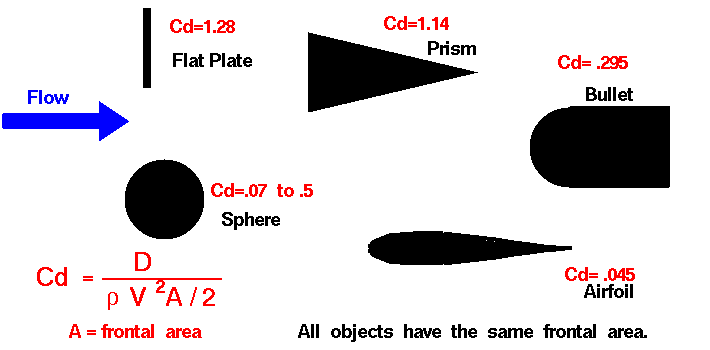
Drag coefficients for various shapes with equivalent frontal area. Image: NASA ( !!!error: Indecipherable SUB-paragraph formatting!!! ).
For the bottom of the car, we can just take 80% of the floorplan outline as the frontal area, since the HyperSport isn't particularly rectangular in top-down view. This gives us 6.97 sq. meters. For the Cd of the bottom, we have to get a bit creative. NASA has a handy, if rudimentary, chart showing the drag coefficients for a number of basic shapes. Let's say that the Lykan is somewhere between a 3D flat sheet and a triangular prism in shape, which would give it a Cd of around 1.2.
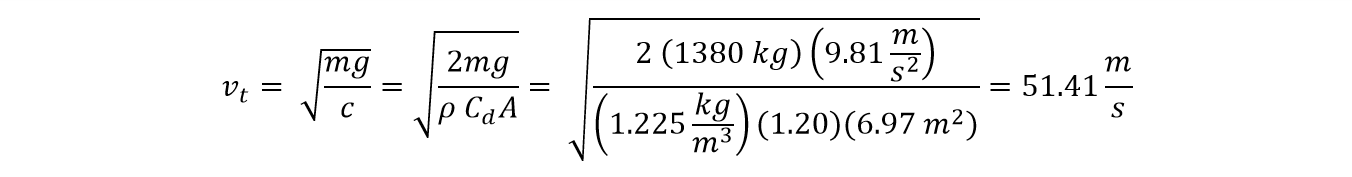
So once we get all of our constants sorted out, we can plug them into the equations and go. Here again, we have to turn our x-axis equation around to solve for t.

And once we do that, it becomes pretty easy to find that our time of flight when factoring air resistance is equal to 2.307 seconds, or barely more than our flight time was when neglecting air resistance. Because both the time as well as the drag area are very low, the impact of air resistance on the travel in the x direction is pretty low.
Even though our flight time is longer, the fallen distance in the y-direction is slightly increased to 25.28 meters, but pretty close to our previous value of 25.13 meters. In a case of a 2.31 second duration without air resistance, we would see a y-direction travel of 26.09 meters, so clearly we can see the effects of the air resistance here.
If you watched the movie, you may remember that halfway between the first tower and the second tower, the car gets hit by a rocket propelled grenade fired by [redacted]. The car is supposed to be bulletproof, but I don't think it's grenade-proof. As such, I've omitted this from my calculations. Because in the real world, if you get hit by a grenade while your car is flying between two skyscrapers, let's face it, you're pretty much screwed. Let's not get too crazy here.
Cover image: screenshot of the Lykan HyperSport mid-flight from the Furious 7 trailer. Image: Universal Studios ( !!!error: Indecipherable SUB-paragraph formatting!!! ).
 MarquetteLa
> Torquelife
MarquetteLa
> Torquelife
04/15/2015 at 16:40 |
|
This is an incredible break-down. Thank you for this.
 ADabOfOppo; Gone Plaid (Instructables Can Be Confusable)
> Torquelife
ADabOfOppo; Gone Plaid (Instructables Can Be Confusable)
> Torquelife
04/15/2015 at 16:45 |
|
Yes, but you didn't factor in them changing gear while driving sliding crashing in a spectacularly controlled manner through the second tower.
As we have all learned from the previous installments of this series, shifting makes everything better.
 Chuck 2(O=[][]=O)2
> Torquelife
Chuck 2(O=[][]=O)2
> Torquelife
04/15/2015 at 16:52 |
|
I mean, you went into a deep analysis of this, yet no one mentions that Vin just picks up the car.
 deekster_caddy
> Torquelife
deekster_caddy
> Torquelife
04/15/2015 at 16:52 |
|
Haven't seen the movie yet. But if the rocket propelled grenade hits near the rear of the car, it's like TURBO BOOST! (minus the bit about how the shrapnel does not contain enough mass to effectively change the speed or trajectory of the much larger car)
Plus, we can now use this to describe it:

Thanks for the great write-up!
 RamblinRover Luxury-Yacht
> Torquelife
RamblinRover Luxury-Yacht
> Torquelife
04/15/2015 at 16:56 |
|
*Waits for FP*
 SmoresTM Has No Chill (O==[][]==O)
> Chuck 2(O=[][]=O)2
SmoresTM Has No Chill (O==[][]==O)
> Chuck 2(O=[][]=O)2
04/15/2015 at 17:05 |
|
Do you doubt Vin Diesel's ability to lift the front end of a 3,042lb car by exerting force onto two small pieces of carbon fiber without anything breaking? How dare you doubt Vin Diesel. You should be ashamed.
 Chuck 2(O=[][]=O)2
> SmoresTM Has No Chill (O==[][]==O)
Chuck 2(O=[][]=O)2
> SmoresTM Has No Chill (O==[][]==O)
04/15/2015 at 17:09 |
|
Wait, hold on. You are forgetting that the car was ALSO bulletproof (to some degree) AND could still reach 243MPH. Wow, what a car. What a guy. During the quick buildup I kept asking, where's the floor jack? Welp, don't need one when you have the guy that stomps on the ground and makes it crumble beneath him.
 sebdel
> Torquelife
sebdel
> Torquelife
04/15/2015 at 17:46 |
|
Great article, very detailed.
One question, does the air resistance varies according to height? doing this at sea level or 9000 up in the mountains would produce any significant changes?
 195100003
> Torquelife
195100003
> Torquelife
04/15/2015 at 17:51 |
|
When I saw the movie, the death of that car was very much on screen and very much destructive.
 Bryan doesn't drive a 1M
> Chuck 2(O=[][]=O)2
Bryan doesn't drive a 1M
> Chuck 2(O=[][]=O)2
04/15/2015 at 18:10 |
|
Welp, don't need one when you have the guy that stomps on the ground and makes it crumble beneath him.
That was my favorite part of any movie in the last 10 years. "The streets always win."
 Tohru
> Torquelife
Tohru
> Torquelife
04/15/2015 at 18:38 |
|
This is good Oppo.
 Raidiar
> Torquelife
Raidiar
> Torquelife
05/29/2018 at 16:54 |
|
Hi torquelide could you show how you got 2.307 seconds for the equation with drag forces. I tried to plug in numbers but I got calculator overload, thanks.